Coding a classic MS-DOS fire demo in 256 bytes

After messing around with x86 Assembly for the B-17 data decompressor, I had the desire to code one of those classic fire demos -
like the PSX Doom fire effect[archive].
Many years ago, when learning to program, I followed a series of tutorials, in .TXT format, to write one, the tutorials were for x86 Assembly but I coded mine in C with Allegro. Now I have come full circle I guess.
Making a palette
First and most important to a good looking fire effect is the palette.
Instead of copying an existing one, I figured mine procedurally. First I grabbed a random fire photo from google.
Next I converted this image to 256 colours indexed format, and sorted the colours by luminance, in Aseprite.
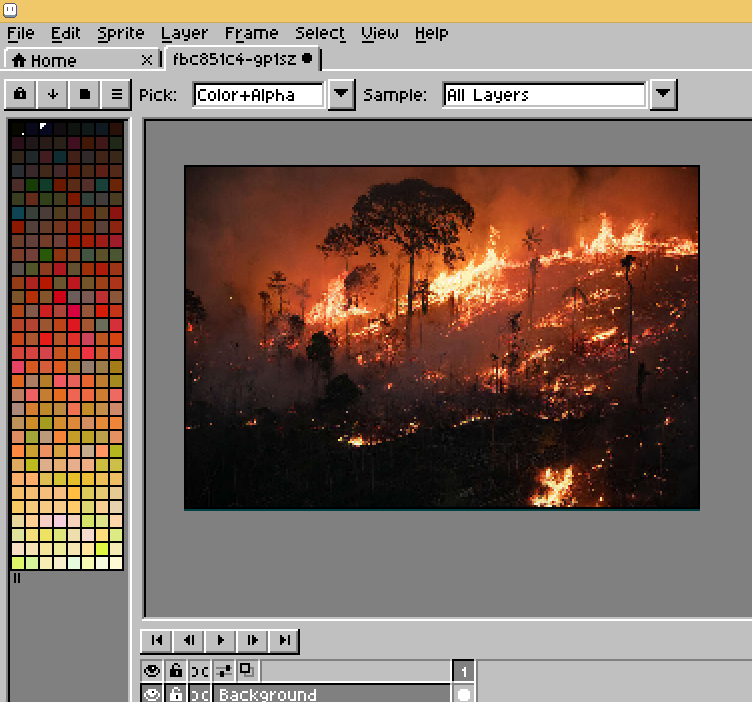
I then exported the palette, to .PAL format, which looks like this:
JASC-PAL
0100
256
0 0 0
8 8 0
8 8 24
8 8 32
16 12 16
16 20 16
16 24 24
16 24 32
41 16 8
41 16 24
32 24 24
41 28 24
41 32 24
65 16 32
...
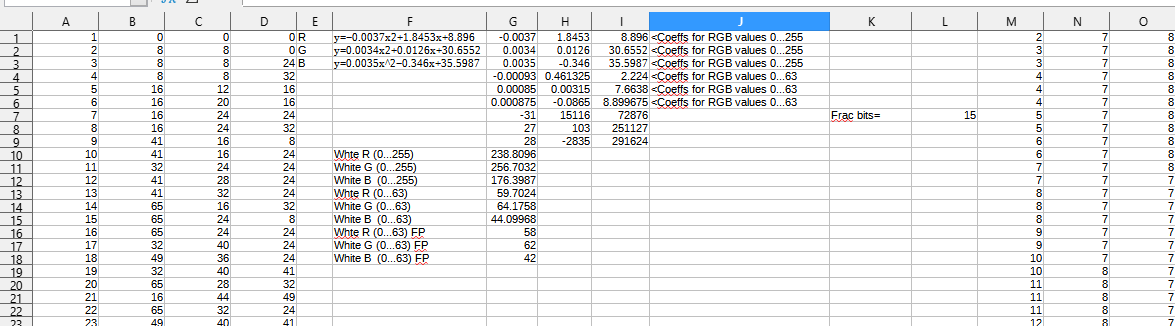
Those values were then passed through a polynomial regression, to create functions from X=[colour index] to Y=[R,G,B].
Thus the palette can be encoded in a very efficient format.
Skeleton of a mode 13h demo
This is the bare skeleton of a mode 13h .COM MS-DOS program.
- Set up a double buffer
- Enter mode 13h
- Upload the palette
- Draw a frame to the buffer
- Upload the buffer to video memory
- Check for a key press, if not pressed, go draw another frame
- Before exiting, restore text mode
The only noteworthy bit is allocating an extra segment to hold the double buffer in RAM.
There are safe methods with error checking to allocate as much memory is necessary in a COM program, however in a 256-byte demo we just assume at least another 64k are available.
use16
segment code
org 100h
mov bp,cs
lea ax,[bp+4096]
mov es,ax
mov ax,13h
int 10h
mov dx,3C8h
xor al,al
out dx,al
xor ebx,ebx
.colloop:
.rgbloop:
mov dx,3C9h
out dx,al
.frame:
push 0xA000
pop es
xor si,si
xor di,di
mov cx,320*200
cld
rep movsb
push ds
pop es
mov ah,0Bh
int 21h
or al,al
jz .frame
die:
mov ax,03h
int 10h
retuse16
segment code
org 100h
;Find a seg 64k above our own
mov bp,cs
lea ax,[bp+4096]
mov es,ax
;Enter mode 13h
mov ax,13h
int 10h
;Prepare to palette upload
mov dx,3C8h
xor al,al
out dx,al
xor ebx,ebx
.colloop:
.rgbloop:
;Calculate a R,G,B component in DX
mov dx,3C9h
out dx,al ;Upload colour component to VGA
;Repeat 3 times...
;[...]
;Repeat 256 times...
;[...]
.frame:
;Do something to update the frame buffer here
;[...]
;Transfer double buffer segment to VGA memory
push 0xA000
pop es ;ES=VGA
xor si,si
xor di,di
mov cx,320*200
cld
rep movsb
push ds
pop es ;ES=double buffer
;Check for keypress
mov ah,0Bh
int 21h
or al,al
jz .frame
die:
;Restore text mode
mov ax,03h
int 10h
;Quit
ret
Running fixed point polynomials
Actually generating the palette is very simple, it is done in 32bit fixed point with 15bits fractional part. More than 15bits would cause overflow.
It can also be done in 16bits fixed point with 11bits fractional part but then the hotter colours look much duller.
The coefficients are stored as such:
fracbits: equ 15
palCoeffs:
dd -31,15116, 72876
dd 27, 103, 251127
dd 28, -2835, 291624
palCoeffsEnd:fracbits: equ 15
;[...]
palCoeffs:
; ;A B C
dd -31,15116, 72876 ;R
dd 27, 103, 251127 ;G
dd 28, -2835, 291624 ;B
palCoeffsEnd:
And then the full loop is as follows:
xor ebx,ebx
.colloop:
mov si,palCoeffs
inc ebx
.rgbloop:
mov eax,ebx
imul ebx
imul dword [si]
push eax
mov eax,ebx
imul dword [si+4]
add eax,dword [si+8]
pop ecx
add eax, ecx
shr eax,fracbits
add si,12
mov dx,3C9h
out dx,al
cmp si,palCoeffsEnd
jb .rgbloop
or bh,bh
jz .colloop xor ebx,ebx
.colloop:
mov si,palCoeffs ;Move SI to A for Red
inc ebx
.rgbloop:
;Calc A*x²
mov eax,ebx ;Load X
imul ebx ;Calc X^2
imul dword [si] ;Calc A*X^2
push eax ;Push result
;Calc B*x
mov eax,ebx ;Load X
imul dword [si+4] ;Calc B*X
;Calc A*x²+B*x+C
add eax,dword [si+8];Add C
pop ecx
add eax, ecx ;Add A*X^2
shr eax,fracbits ;Discard fractional part of fixed point
add si,12 ;Move SI to next A coeff
mov dx,3C9h
out dx,al ;Upload colour component to VGA
cmp si,palCoeffsEnd ;If all coeffs were used then this colour is done
jb .rgbloop
or bh,bh
jz .colloop
Random number generation
The procedural fire effect requires random numbers in a few different places.
One of the simplest and most compact Random Number Generators is the Lehmer RNG.
I picked the coefficient from "TABLES OF LINEAR CONGRUENTIAL GENERATORS OF DIFFERENT SIZES AND GOOD LATTICE STRUCTURE", an article with tables of several possible ones.
Note how I use the segment override, this is because in the rest of the code DS is often pointing to the double buffer.
randomByte:
mov eax,851723965
mul dword [cs:rng]
mov [cs:rng],eax
shr eax,24
ret
rng: dd 1randomByte:
;RNG subroutine of Lehmer kind
mov eax,851723965
mul dword [cs:rng]
mov [cs:rng],eax
shr eax,24
ret
rng: dd 1
The actual fire effect
The meat of the fire effect is very simple.
The fire is seeded by a line of "ambers", metaphorically and algorithmically, that is a line of random bright pixels:
mov di,320*200
push di
mov cx,320
.fill:
call randomByte
or al,1<<7
stosb
loop .fill ;Fill an invisible line below the screen with random values 128...255
mov di,320*200
push di
mov cx,320
.fill:
call randomByte
or al,1<<7
stosb
loop .fill
Then, for every pixel in the screen; move it up, and cool it a bit. The full algorithm is described in Fabien Sanglard's PSX Doom fire effect page[archive].
xor di,di
pop cx
.pixel:
add di,51051
cmp di,320*200
jnb .pixel
call randomByte
mov dl,3
mul dl
shr ax,8
lea si,[di+319]
add si,ax
call randomByte
mov dl,al
lodsb
and dx,15
sub dx,4
sub ax,dx
jns .notneg
xor al,al
.notneg:
stosb
loop .pixel xor di,di
pop cx ;CX=320*200
.pixel:
;Update pixels in a "random" order
add di,51051
cmp di,320*200
jnb .pixel
;Find address of a pixel a line below, and maybe 1 pixel to either side
call randomByte
mov dl,3
mul dl
shr ax,8
lea si,[di+319]
add si,ax
;Get pixel, cool it down by a random value
call randomByte
mov dl,al
lodsb
and dx,15
sub dx,4
sub ax,dx
jns .notneg
xor al,al
.notneg:
;Store new pixel
stosb
loop .pixel
I will only add that the order of pixel updates matters a lot. If one removes the bit which adds 51051 (3 × 11 × 7 × 13 × 17 = coprime both to 320 and to 200), the result is a very patterned, unnatural fire:

The result
The final result is 234 bytes - under the 256 byte target - and even 2152 bytes less than the source code.
The GIFs dont do it justice - you can download source and COM file here:
 | DOWNLOAD XTRACT UTILITY |





